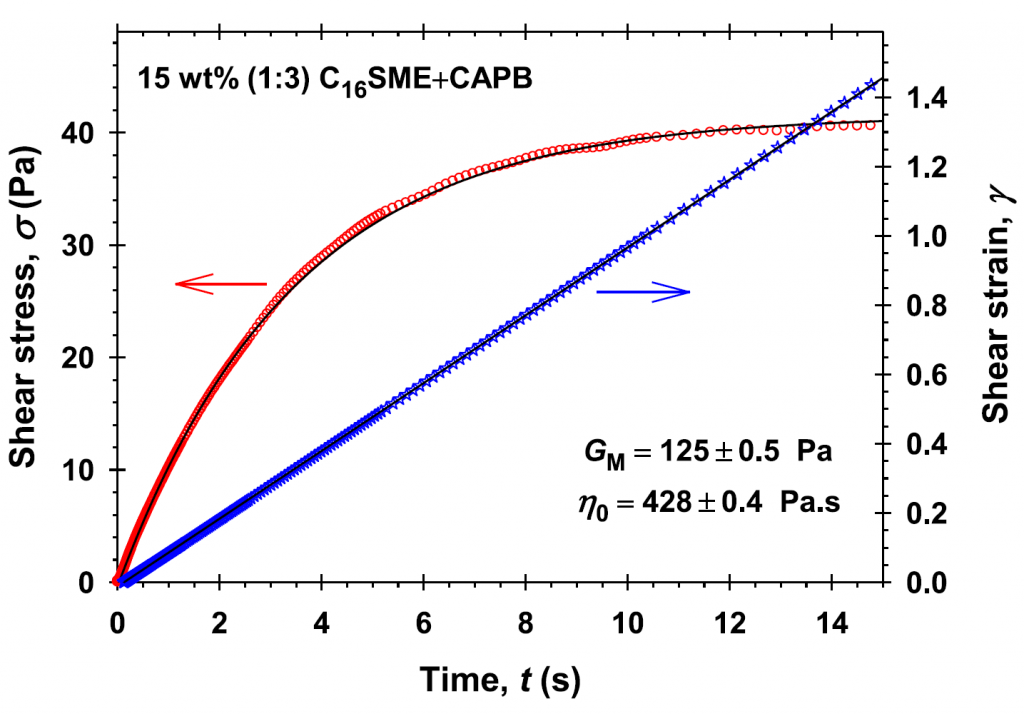
The shear rheology of linear wormlike micellar solutions (WMSs) is described by both Poisson renewal (PRM)and shuffling (SFM) models with different values of the model parameters. For low shear strains and rates ofstrains, the micellar solutions behave as a Maxwellian body with constant elasticity and viscosity. The excellentdescription of experimental data in the literature using PRM or SFM suggests that both models predict identicaldependencies of the dynamic storage and loss moduli on the frequency of oscillations. It is shown in the literature, that the PRM becomes equivalent to the SFM, when the breaking time is constant, τbr, and the characteristic reptation time, τrep, is equal to π2 τd0, where τd0 is the reptation time evaluated with respect to the average length of the chain. Three independent rheological tests (apparent viscosity vs shear rate, stress vs strain at constant shear rates, strain oscillations at low amplitudes and different frequencies) are applied to low, medium, and high zero-shear viscosity WMSs to obtain the PRM and SFM model parameters (elasticity, viscosity, relaxation, breaking, and reptation times). The known closed-form analytical expression for the Laplace image of the stress relaxation function and the respective infinite series for the complex modulus give possibility for the reported here precise systematic calculations of the storage and elastic moduli, the crossover frequency, and the elasticity for all values of ζbr = τbr/τrep ≤ 100. The predictions of the PRM length-dependent breaking-time versions are indistinguishable from those of the SFM for the obtained universal dependencies of the characteristic time, τB0, on ζbr. The applicability of the Vasquez–Cook–McKinley and the single-mode Oldroyd 8-constant models to describe the rheological behavior of WMSs is tested. The theoretical findings and conclusions are confirmed experimentally and illustrate the self-consistency of the used rheological regimes.