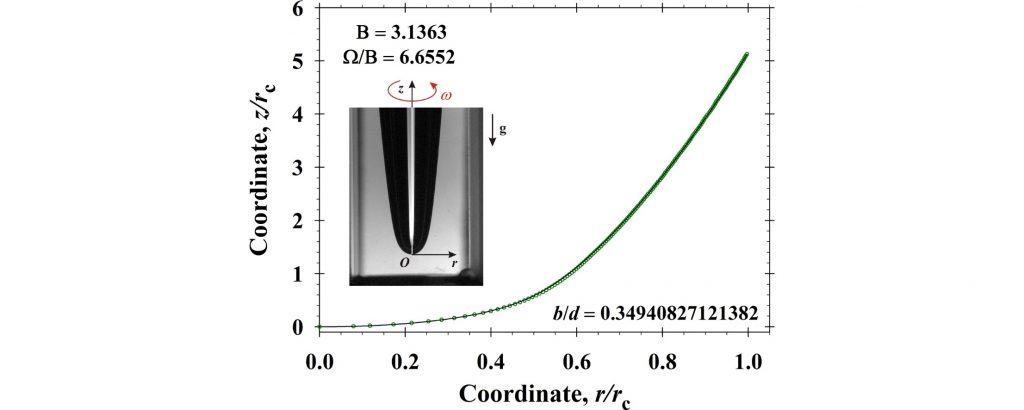
The classical axisymmetric drop shape analysis (ADSA) method is used to measure the surface tensions and contact angles from the best fit of drop images with the Young–Laplace equation of capillarity. To produce well deformed drops needed for better precision, one applies rotation with a sufficiently high angular velocity in addition to the gravitational field. Without rotation, the conventional fourth-order Runge–Kutta and second-order Taylor methods are suitable for obtaining the numerical solution of the Young–Laplace equation required for ADSA, but they are slow for the case of a rotating drop in gravitational field. The real-time data processing of images of rotating drops requires relatively simple, high-precision, and stable numerical methods working with a well-defined fixed computational time. This study aims to develop the sixth-order Taylor method (T6) for the specific problem and to compare its accuracy, stability, and computational time with the available classes of Runge–Kutta (fifth-, sixth-, tenth-orders, and second-order 3-stage method with step control), Adams–Bashforth (sixth- and seventh-orders), and predictor-corrector methods based on the seventh-order Adams–Moulton approach (PC76 and PC77). The ranges of stability of these methods under variation of the parameters characterizing the capillary profiles are obtained and their computational times, tested on the experimental data for rotating drops in gravitational field, are compared. From the viewpoint of real-time data processing, the most appropriate methods are T6, PC76, and PC77 because of their high precision, good stability, and sufficiently short predictable computational times.